复杂性平方律

系统的复杂性正比于系统规模的平方

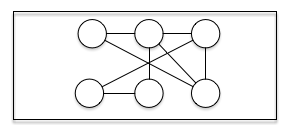
一、系统的复杂性不仅由节点的数量（即“规模”）带来，更多的是由节点间的关系（包括没有关系）带来。 这也就是复杂性平方律的原因。系统的复杂性正比于节点数的平方，因为节点间的连接数正比于节点数的平方。 我们假设节点和连接的复杂度都为1，比如下图所示的系统，总复杂度为14。

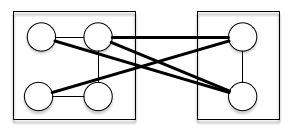
二、尝试分拆系统。节点被分拆到两个不同的空间，出现了跨空间的连接，这些连接通常成本相对高，带来了相当多额外复杂度。 所以简单的分割不一定能带来复杂性的改善。 我们假设跨空间连接的复杂度为k，则两个空间的复杂度分别为7+4k、3+4k，要使分拆后复杂度降低，对k的要求很高 -

7 + 4k < 14 => k < 1.75

3 + 4k < 14 => k < 2.75

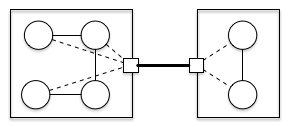
三、增加一些节点和连接（方块节点和虚线连接）来改变跨空间连接。 由于方块节点和虚线连接通常是一些技术性的代理元素，不用承载领域内容。它们的复杂性通常小于普通元素。这里我们仍然按1来计算。 同样计算对k的要求，发现降低了很多。

11+ k < 14 => k < 3

6 + k < 14 => k < 8

（待续） ¹